Bubble dynamics

Depending on forces it experiences, bubbles in a liquid exhibit different kind of motions, including zigzag or spiralling motions, induced by the acoustic radiation force on a single bubble, called the primary Bjerknes force. When bubbles smaller than the resonant radius are located in a standing acoustic wave, they are pushed towards the acoustic pressure antinode and form a bubble cluster. For bubbles larger than the resonant size, they naturally move towards the pressure node that can be a ring in a cylindrical geometry (see Figure). This simple view in linear acoustic does not take into account the possible coupling between bubble translation and their radial oscillation, coupling that appears in sufficiently strong acoustic field. In this case, bubbles smaller than the resonant size can concentrate around the pressure node that corresponds to the stable equilibrium location for large bubbles. The existence and combination of the two radial and longitudinal modes propagating in the resonator allows the possibility for small bubbles to coexist with larger bubbles in the vicinity of their linearly unstable equilibrium location through orbital or spiralling motions.

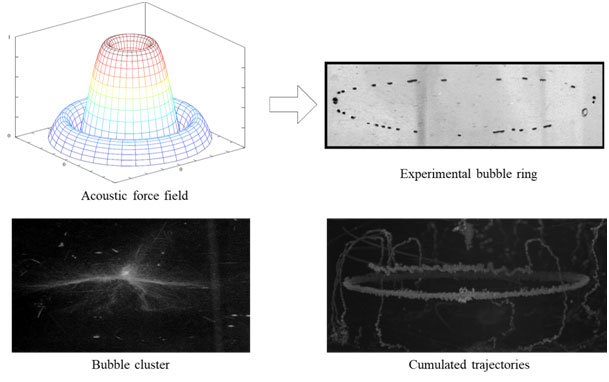
Fig1 – Experimental observations of the positional stability location of acoustic bubbles according to their size and the acoustic force field: bubbles smaller than resonant size moves towards a pressure antinode (bubble cluster) and those larger moves towards the pressure node (here a bubble ring)

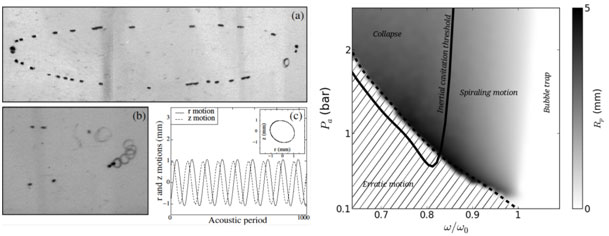
Fig2 – Left: Snapshot of spiralling motion of small bubbles around their initially unstable equilibrium location (the bubble ring) and the associated numerical investigation of the bubble translational motion. Right: Characterization of the frequency-pressure amplitude phase space leading to spiralling motion, bubble collapse, bubble trapping and erratic motion.

LabTau Staff

• Matthieu Guédra (Postdoc)

• Bruno Gilles (Assoc. Prof.)

• Jean-Christophe Bera (Prof.)

• Claude Inserra (Assoc. Prof.)

Collaborations

• Cyril Desjouy (Assoc. Prof., LMFA, Ecully)

[1] Orbital trajectory of an acoustic bubble in a cylindrical resonator. C Desjouy, P Labelle, B Gilles, JC Bera, C Inserra. Physical Review E, 88:033006, 2013.

[2] Acoustic bubble behaviour in a standing wave field. C Desjouy, P Labelle, B Gilles, JC Bera, C Inserra. Proceedings on Meetings on Acoustics, 19(1):045010, 2013.

When submitted to an acoustic field, a gas bubble behaves like a pulsating sphere. For sufficiently high pressure amplitude, above a given pressure threshold, the gas/liquid interface becomes unstable and the bubble deforms from its commonly-observed spherical shape. This instability is ruled by the amplitudes of the spherical oscillations of the microbubble, similarly to a Faraday instability. In this research axis we focus on the experimental observation and theoretical understanding of the nonspherical oscillations of bubbles. The capture of the shape deformations of microbubble is obtained by the trapping of single bubbles (nucleated by a focused laser beam) in a water tank. Once trapped, bubbles are imaged by a high-speed camera (180 kfps) allowing the capture of the dynamics within an acoustic period of the oscillation. In order to evaluate the bubble contour and relative weight of non-spherical modes, the bubble interface is expanded over the Legendre polynomial series P_n(cos(θ)). This allows extracting the dynamics of each a_n-component of the n-th excited non spherical mode. Experimental observations reveal that, in addition to the expected parametric instability of a predominant surface mode, others modes can coexist and appear through nonlinear coupling between the spherical, nonspherical and translational modes of the bubble. Such energy transfer between modes has been for the first time dynamically resolved [1,2], and opens the way to a potential shape-to-volume mode modification effect, theoretically predicted but never observed yet. By increasing acoustic pressure we reported such effect for a 68 µm bubble undergoing both significant translational oscillations and triangular shape deformations. The ability of higher-order modes to significantly alter the spherical mode (with application to enhancement of UCA’s echogenicity) has been demonstrated.

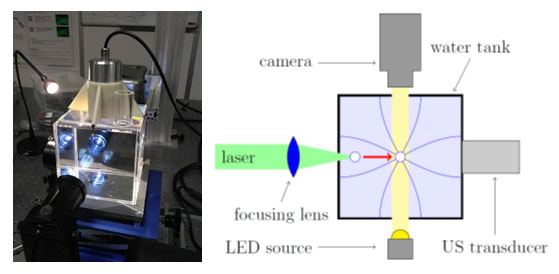
Fig1 - Left: photograph of the experimental setup. Right: Principle of the ultrasound trapping technique of a laser-nucleated single bubble.

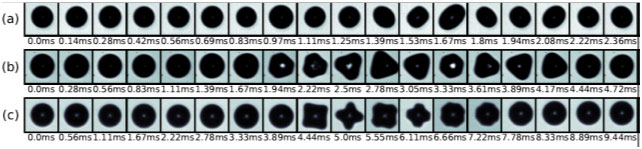
Fig2 - Snapshot of resulting shape deformations during one half period of the acoustic modulation for a (a) 48, (b) 68 and (c) 57 µm bubble radius.

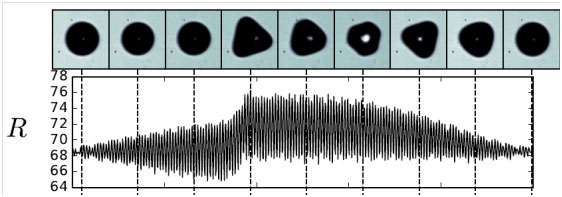
Fig3 - Temporal evolution of the spherical mode oscillations over a modulation period, highlighting the ability of higher-order modes to significantly alter the spherical mode.

[1] Periodic onset of bubble shape instabilities and their influence on the spherical mode. M Guedra, C Inserra, C Mauger, B Gilles. IEEE Transactions in Ultrasonics, 2016.

[2] Experimental evidence of nonlinear mode coupling between spherical and nonspherical oscillations of microbubbles. M Guedra, C Inserra, C Mauger, B Gilles. Physical Review E, 94: 053155, 2016.

[3] Time-resolved dynamics of micrometer-sized bubbles undergoing shape oscillations. M Guédra, S Cleve, C Mauger, C Inserra, P Blanc-Benon. Proceedings on Meetings on Acoustics, 141(5): 3493, 2017.

In the context of sonoporation, we use supported lipid bilayers as a model of biological membranes and investigate the interactions between the bilayer and microbubbles induced by ultrasound. When applying ultrasound and generating microbubbles above a supported biomimetic membrane, a bubble cloud both in transmission and fluorescent images (figure 1), indicating that bubbles collect fluorescent lipid from the bilayer. By recording the vicinity of the bubble cloud with an epifluorescence microscope equipped with a fast sensitive camera, we could observe the very fascinating behaviour of jumping bubbles on the bilayer, forming a necklace pattern of alteration on the membrane. By capturing more precisely the bubble dynamics, we found that these cavitating bubbles are regularly pumping lipids from the bilayer, allowing the entrance of water below the bubble, reducing its adhesion, and finally jumping to a nearby location with a noticeable regularity (figure 2). Qualitatively these instabilities result from a competition between downward oriented van der Waals and Bjerknes forces on one hand, and upward hydrodynamic lift forces on the other hand (figure 3).

Fig1: Experimental observations of the interaction between acoustic bubbles (right, natural light) and fluorescent bilayer membranes (left) mimicking cell biological membranes.

Fig2: Left: Successive temporal snapshots of a jumping bubble on the bilayer membrane. Right: Resulting necklace patterns illustrating the jumping phenomenon.

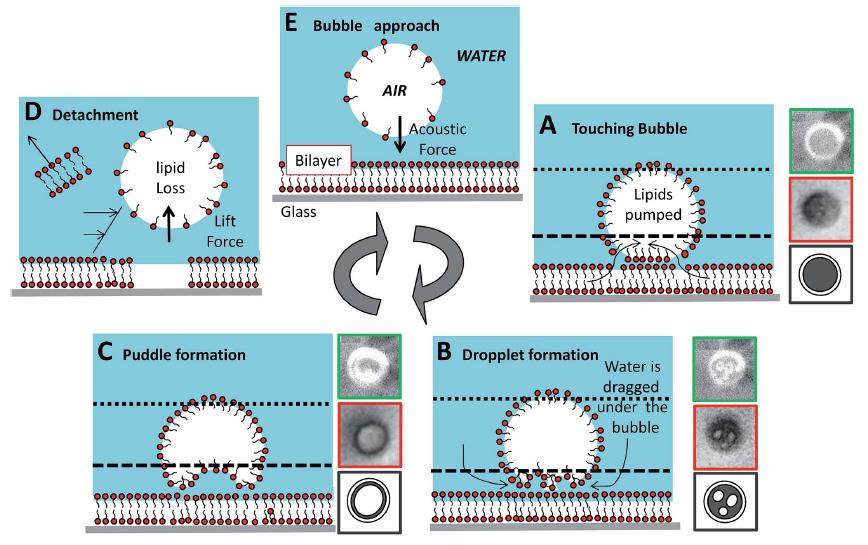
Fig3: Process mechanism for the jumping phenomenon.

• Monitoring and control of inertial cavitation activity for enhancing ultrasound transfection: the SonInCaRe project. C Inserra, P Labelle, C Der Loughian, JL Lee, M Fouqueray, J Ngo, A Poizat, C Desjouy, B Munteanu, CW Lo, C Vanbelle, JP Rieu, WS Chen, JC Bera. IRBM, 35(2): 94-99, 2014.
• Jumping acoustic bubbles on lipid bilayers. C Der Loughian, P Muleki-Seya, C Pirat, C Inserra, JC Bera, JP Rieu. Soft Matter, 11: 3460-69, 2015.
• Proceeding